How to Calculate Vertical Capsule Tank Volume

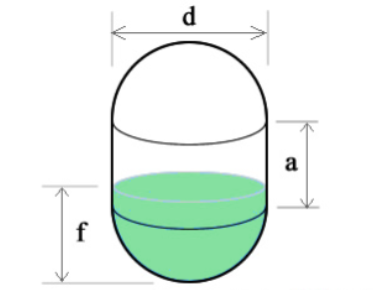
To calculate the volume of a vertical capsule tank, we treat the capsule as a combination of a sphere and a cylinder. The capsule consists of two hemispherical ends and a cylindrical section in the middle. The diameter of the capsule is denoted as \( d \), and the radius \( r \) is equal to \( \frac{d}{2} \). The height of the cylindrical section is denoted as \( a \), while the height of each hemispherical end is also \( r \).

The total volume of the capsule tank, denoted as \( V_{\text{capsule}} \), can be calculated using the following formula:

To calculate the fill volume of a vertical capsule tank, we will use similar methods as for a vertical oval tank. Specifically, the spherical cap method and the volume of the cylinder are used depending on the fill height \( f \). Below are the detailed steps based on different fill heights.

• When fill height \( f < r \):

  In this case, the tank is partially filled within one of the hemispherical ends. We use the spherical cap formula to calculate the volume of the filled part. The formula for the volume of a spherical cap is:

  \[ V_{\text{spherical cap}} = \frac{1}{3} \pi h^2 (3R - h) \]

  Where:

  • R = radius of the spherical cap (in this case, \( r \))
  • h = height of the spherical cap (in this case, the fill height \( f \))

  Thus, the fill volume is simply the volume of the spherical cap:

  \[ V_{\text{fill}} = V_{\text{spherical cap}} \]

• When \( r < f < (r + a) \):

  In this case, the fill height \( f \) has reached the cylindrical section and part of one hemisphere. The total fill volume is the sum of two parts:

  • The volume of half the sphere, given by:

  \[ V_{\text{half sphere}} = \frac{2}{3} \pi r^3 \]

  • The volume of the fill inside the cylinder, given by:

  \[ V_{\text{cylinder fill}} = \pi r^2 (f - r) \]

  Therefore, the total fill volume is:

  \[ V_{\text{fill}} = V_{\text{half sphere}} + V_{\text{cylinder fill}} = \frac{2}{3} \pi r^3 + \pi r^2 (f - r) \]

• When \( (r + a) < f < h \): (where \( h \) is the total height of the capsule tank, i.e., the sum of the two hemispheres and the cylindrical section)

  In this case, the fill height \( f \) has passed the cylindrical section and may partially fill the top hemisphere. We calculate the volume of the filled portion by using the spherical cap method for the remaining portion of the top hemisphere. However, it's often simpler to calculate the total filled volume directly:

  \[ V_{\text{fill}} = V_{\text{capsule}} - V_{\text{spherical cap of empty part}} \]

  Here, \( V_{\text{spherical cap of empty part}} \) is the volume of the empty portion in the top hemisphere, which can be calculated using the spherical cap formula by substituting \( h - f \) for the height of the cap.

  In practice, it’s more common to calculate the total volume up to the fill height without first calculating the empty portion, especially when \( f \) exceeds the height of the cylindrical section.

Note: If \( f \) exceeds the total height \( h \) of the capsule tank, then the fill volume will equal the total volume of the capsule. However, this situation is rare as the fill height typically does not exceed the design height of the tank.