Sphere Volume Calculator - Calculate volume in litres, gallons, cubic feet, bbl, cubic meters

Sphere Volume (m³):

Filled Volume (m³):

Sphere Volume (U.S. Gallons):

Filled Volume (U.S. Gallons):

Sphere Volume (Imp. Gallons):

Filled Volume (Imp. Gallons):

Sphere Volume (Liters):

Filled Volume (Liters):

Sphere Volume (Cubic Feet):

Filled Volume (Cubic Feet):

Sphere Volume (bbl):

Filled Volume (bbl):

Sphere Volume Formula

Volume Calculation

The volume of a sphere is calculated using the formula:

\(V_{\text{sphere}} = \frac{4}{3}\pi r^3\)

Where:

r = radius of the sphere

This formula calculates the total volume enclosed by a perfect sphere. The volume increases rapidly as the radius increases due to the cubic relationship between the radius and the volume.

Example Calculation

If a sphere has a radius of 3 meters, its volume would be calculated as:

\(V_{\text{sphere}} = \frac{4}{3} \pi (3)^3 = \frac{4}{3} \pi (27) = 36 \pi \approx 113.1 \, \text{m}^3\)

This means the sphere would occupy approximately 113.1 cubic meters of space.

Volume of Spherical Cap

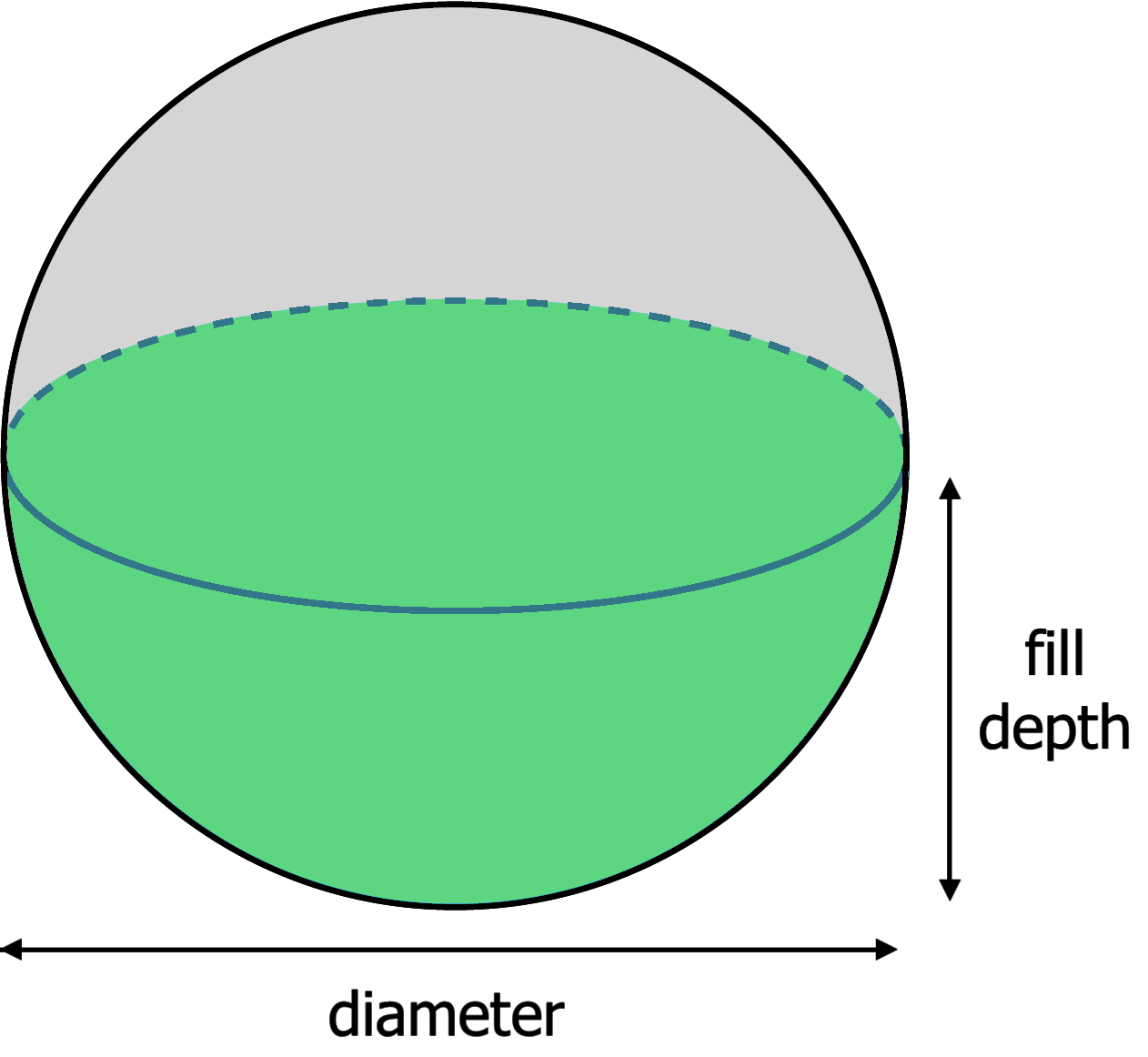
The volume of a spherical cap is calculated using the formula:

\(V_{\text{spherical cap}} = \frac{1}{3}\pi h^2(3R - h)\)

Where:

R = radius of the sphere
h = height of the spherical cap

A spherical cap is the portion of a sphere that is "cut off" by a plane. The formula calculates the volume of this portion, where h is the height of the cap and R is the radius of the sphere. The formula can be used to determine the volume of a dome-like section of a sphere.

Example Calculation for Spherical Cap

If the radius of the sphere is 5 meters and the height of the spherical cap is 2 meters, the volume of the spherical cap would be:

\(V_{\text{spherical cap}} = \frac{1}{3} \pi (2)^2 (3(5) - 2) = \frac{1}{3} \pi (4) (15 - 2) = \frac{1}{3} \pi (4) (13) = \frac{52}{3} \pi \approx 54.7 \, \text{m}^3\)

The volume of the spherical cap in this example would be approximately 54.7 cubic meters.