Horizontal Cylinder Tank Volume Calculator - Calculate volume in litres, gallons, cubic feet, bbl, cubic meters

Total Volume (m³):

Filled Volume (m³):

Total Volume (U.S. Gallons):

Filled Volume (U.S. Gallons):

Total Volume (Imp. Gallons):

Filled Volume (Imp. Gallons):

Total Volume (Liters):

Filled Volume (Liters):

Total Volume (Cubic Feet):

Filled Volume (Cubic Feet):

Tank Volume (bbl):

Filled Volume (bbl):

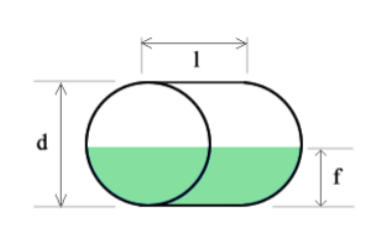
Total and Filled Volume of a Horizontal Cylinder Tank

The total volume \( V_{\text{tank}} \) of a cylindrical tank can be calculated by multiplying the area \( A \) of its circular base by its length \( l \). The area \( A \) of the circular base is determined using the formula \( \pi r^2 \), where \( r \) is the radius of the circular base. The radius \( r \) is half the diameter, i.e., \( r = \frac{d}{2} \). Therefore, the total volume of the tank is expressed as:

\( V_{\text{tank}} = \pi r^2 l \)

Here, \( d \) represents the diameter of the circular base, \( r \) is the radius, and \( l \) is the length of the tank.

Filled Volume of a Horizontal Cylinder Tank

To determine the filled volume of a horizontal cylindrical tank, the area \( A \) of the circular segment representing the filled portion must be calculated and then multiplied by the length \( l \) of the tank. The circular segment's area \( A \) depends on the central angle \( \theta \) and the sine of this angle.

The area \( A \) of the circular segment is given by:

\( A = \frac{1}{2} r^2 (\theta - \sin\theta) \)

In this formula, \( \theta \) is measured in radians and is determined using the following relationship:

\( \theta = 2 \arccos\left(\frac{r}{m}\right) \)

Here, \( m \) represents the vertical distance from the center of the circular base to the chord that defines the base of the circular segment. The chord corresponds to the boundary of the filled or unfilled section of the tank.

Consequently, the volume of the circular segment, \( V_{\text{segment}} \), can be expressed as:

\( V_{\text{segment}} = \frac{1}{2} r^2 (\theta - \sin\theta) l \)

Case 1: Fill Height Less Than Half the Diameter

When the fill height \( f \) is less than half the diameter \( d \) (i.e., \( f < \frac{d}{2} \)), the filled portion corresponds directly to the segment described above. Therefore, the filled volume \( V_{\text{fill}} \) is equal to the volume of the segment:

\( V_{\text{fill}} = V_{\text{segment}} \)

Case 2: Fill Height Greater Than Half the Diameter

If the fill height \( f \) exceeds half the diameter \( d \) (i.e., \( f > \frac{d}{2} \)), the filled portion can be determined by subtracting the volume of the empty segment from the total volume of the tank. In this case, the filled volume \( V_{\text{fill}} \) is:

\( V_{\text{fill}} = V_{\text{tank}} - V_{\text{segment}} \)

Here, \( V_{\text{segment}} \) represents the volume of the empty portion of the tank.

This method ensures accurate calculation of the filled volume for any given fill height \( f \), whether it is less than or greater than half the tank's diameter.