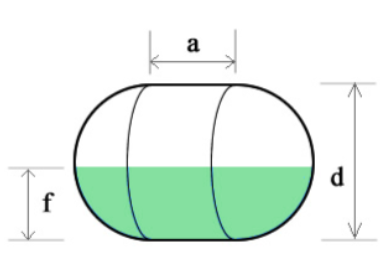
A horizontal capsule tank is defined as a combination of a cylinder, with height \(a\) and diameter \(d\), and two hemispherical ends of the same diameter. Here, the radius is \(r = \frac{d}{2}\).

Key Volume Formulas

The volume of a sphere is given by:

\(V_{\text{sphere}} = \frac{4}{3} \pi r^3\).

The volume of a cylinder is:

\(V_{\text{cylinder}} = \pi r^2 a\).

Therefore, the total volume of the capsule tank, including the cylinder and two hemispherical ends, is:

\(V_{\text{capsule}} = \pi r^2 \left( \frac{4}{3} r + a \right)\).

Volume of Fill in a Horizontal Capsule

To calculate the volume of liquid in a partially filled horizontal capsule tank, we use separate methods for the cylindrical and hemispherical sections.

1. Liquid Volume in the Cylindrical Section

For the cylindrical section, the liquid forms a circular segment. The area of this segment is calculated as:

\(A_{\text{segment}} = r^2 \cos^{-1}\left(\frac{r-h}{r}\right) - (r-h) \sqrt{2rh - h^2}\),

where \(h\) is the liquid height within the cylinder.

The liquid volume in the cylindrical section is then:

\(V_{\text{cylinder (liquid)}} = A_{\text{segment}} \cdot a\).

2. Liquid Volume in the Hemispherical Ends

For each hemispherical end, the liquid forms a spherical cap. The volume of a spherical cap is given by:

\(V_{\text{spherical cap}} = \frac{1}{3} \pi h^2 (3R - h)\),

where \(R\) is the sphere's radius and \(h\) is the cap height. For the two hemispherical ends, the total liquid volume is:

\(V_{\text{hemisphere (liquid)}} = 2 \cdot \frac{1}{3} \pi h^2 (3r - h)\).

Total Liquid Volume

The total liquid volume in the capsule is the sum of the cylindrical and hemispherical contributions:

\(V_{\text{liquid}} = V_{\text{cylinder (liquid)}} + V_{\text{hemisphere (liquid)}}\).

Common Questions

1. What is the total volume of the tank?

The total volume is: \(V_{\text{capsule}} = \pi r^2 \left( \frac{4}{3} r + a \right)\).

2. How is the liquid volume calculated for a given height?

Use the formulas for \(V_{\text{cylinder (liquid)}}\) and \(V_{\text{hemisphere (liquid)}}\), summing them to find \(V_{\text{liquid}}\).

3. How does the orientation affect volume calculations?

In the horizontal orientation, the liquid volume depends on the geometry of circular segments and spherical caps. In a vertical orientation, the liquid volume is proportional to the height directly.

4. How do you calculate the percentage of the tank filled?

Calculate the fill percentage as: \[ \text{Fill percentage} = \left(\frac{V_{\text{liquid}}}{V_{\text{capsule}}}\right) \times 100. \]

5. What if the liquid height only partially fills the hemispherical ends?

In such cases, use the spherical cap formula for the liquid volume: \(V_{\text{spherical cap}} = \frac{1}{3} \pi h^2 (3r - h)\).

Example Calculation

For a tank with \(d = 2 \, \text{m}\), \(a = 4 \, \text{m}\), and \(h = 1 \, \text{m}\):

• Total volume: \(V_{\text{capsule}} = \pi (1)^2 \left(\frac{4}{3}(1) + 4\right) = \pi \cdot \frac{16}{3} \approx 16.76 \, \text{m}^3\).
• Liquid volume in the cylindrical section: \(V_{\text{cylinder (liquid)}} = \frac{\pi}{2} \cdot 4 = 2\pi \, \text{m}^3\).
• Liquid volume in the hemispherical ends: \(V_{\text{hemisphere (liquid)}} = 2 \cdot \frac{1}{3} \pi (1)^2 (3 \cdot 1 - 1) = \frac{4}{3} \pi \, \text{m}^3\).
• Total liquid volume: \(V_{\text{liquid}} = 2\pi + \frac{4}{3}\pi = \frac{10}{3}\pi \approx 10.47 \, \text{m}^3\).