Dome Roof Oblique Cone Bottom Tank Volume Calculator - Calculate volume in litres, gallons, cubic feet, bbl, cubic meters

Tank Volume (m³):

Filled Volume (m³):

Tank Volume (U.S. Gallons):

Filled Volume (U.S. Gallons):

Tank Volume (Imp. Gallons):

Filled Volume (Imp. Gallons):

Tank Volume (Liters):

Filled Volume (Liters):

Tank Volume (Cubic Feet):

Filled Volume (Cubic Feet):

Tank Volume (bbl):

Filled Volume (bbl):

Tank Volume (bbl):

Filled Volume (bbl):

Dome Roof Oblique Cone Bottom Tank Volume Formula

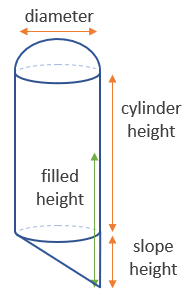
Volume Calculation

The total volume of a dome roof oblique cone bottom tank is determined by summing the volumes of the cylindrical section, the sloped cone section, and the dome section:

Sloped Cone Section Volume

The volume of the sloped cone section is given by:

\[ V_{\text{slope}} = \frac{1}{3} \pi r^2 H_{\text{slope}} \]

Where:

r = Radius (diameter / 2)
H_slope = Height of the sloped cone section

Cylindrical Section Volume

The volume of the cylindrical section is given by:

\[ V_{\text{cylinder}} = \pi r^2 H_{\text{cyl}} \]

Where:

r = Radius (diameter / 2)
H_cyl = Height of the cylindrical section

Dome Section Volume

The volume of the dome section is calculated as a spherical cap:

\[ V_{\text{top}} = \frac{2}{3} \pi r^3 \]

Where:

r = Radius (diameter / 2)

Total Volume

The total volume of the tank is:

\[ V_{\text{tank}} = V_{\text{cylinder}} + V_{\text{slope}} + V_{\text{top}} \]

Filled Volume Calculation

The filled volume of the tank depends on the height of the liquid level:

Case 1: If filled height ≤ slope height:

The filled volume is calculated as:

\[ V_{\text{filled}} = \frac{1}{3} \pi \left(\frac{H_{\text{filled}}}{H_{\text{slope}}}\right) r \left(\frac{H_{\text{filled}}}{H_{\text{slope}}}\right) r H_{\text{filled}} \]

Case 2: If filled height > slope height:

The filled volume includes the cylindrical and sloped cone sections:

\[ V_{\text{filled}} = \pi r^2 (H_{\text{filled}} - H_{\text{slope}}) + V_{\text{slope}} \]

Where:

H_filled = Height of the liquid level
H_slope = Height of the sloped cone section
r = Radius (diameter / 2)

Example Calculation

Suppose the tank has the following dimensions:

Diameter = 6 m
Sloped cone height = 3 m
Cylindrical height = 4 m

1. Calculate the sloped cone section volume:

\[ V_{\text{slope}} = \frac{1}{3} \pi (3)^2 (3) = 9\pi \, \text{m}^3 \]

2. Calculate the cylindrical section volume:

\[ V_{\text{cylinder}} = \pi (3)^2 (4) = 36\pi \, \text{m}^3 \]

3. Calculate the dome section volume:

\[ V_{\text{top}} = \frac{2}{3} \pi (3)^3 = 18\pi \, \text{m}^3 \]

Total Volume:

\[ V_{\text{tank}} = 9\pi + 36\pi + 18\pi = 63\pi \, \text{m}^3 \approx 197.9 \, \text{m}^3 \]

How can I calculate the volume if the tank has an irregular slope?
Use integration techniques or approximate the slope as multiple linear sections and sum their volumes.

What unit conversions are needed for practical applications?
Convert the calculated volume to liters (1 m³ = 1,000 liters) or gallons as required.

Can this formula be applied to tanks with flat tops?
Yes, by omitting the dome section volume \( V_{\text{top}} \).