Dome Roof Cone Volume Calculator - Calculate volume in litres, gallons, cubic feet, bbl, cubic meters

Tank Volume (m³):

Filled Volume (m³):

Tank Volume (U.S. Gallons):

Filled Volume (U.S. Gallons):

Tank Volume (Imp. Gallons):

Filled Volume (Imp. Gallons):

Tank Volume (Liters):

Filled Volume (Liters):

Tank Volume (Cubic Feet):

Filled Volume (Cubic Feet):

Tank Volume (bbl):

Filled Volume (bbl):

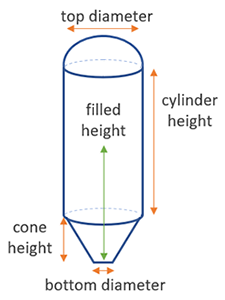
Dome Roof Cone Tank Volume Formula

Volume Calculation

The total volume of a dome roof cone tank is determined by summing the volumes of the cylindrical, conical, and dome sections:

Cylindrical Section Volume

The volume of the cylindrical section is given by:

\[ V_{\text{cylinder}} = \pi r^2 H_{\text{cyl}} \]

Where:

r = Radius of the cylindrical section (diameter / 2)
H_cyl = Height of the cylindrical section

Conical Section Volume

The volume of the conical section is given by:

\[ V_{\text{cone}} = \frac{\pi}{3} H_{\text{cone}} (br^2 + br \cdot tr + tr^2) \]

Where:

H_cone = Height of the conical section
br = Bottom radius (bottom diameter / 2)
tr = Top radius (top diameter / 2)

Dome Section Volume

The volume of the dome section is calculated as a hemisphere:

\[ V_{\text{dome}} = \frac{2}{3} \pi r^3 \]

Where:

r = Radius of the dome section (diameter / 2)

Total Volume

The total volume of the tank is:

\[ V_{\text{tank}} = V_{\text{cylinder}} + V_{\text{cone}} + V_{\text{dome}} \]

Filled Volume Calculation

The filled volume of the tank depends on the height of the liquid level:

Case 1: If filled height ≤ height of the conical section:

\[ R_{\text{cut}} = br + \left(\frac{\text{H}_{\text{filled}}}{H_{\text{cone}}}\right) \cdot H_{\text{cone}} \cdot \left(\frac{tr - br}{H_{\text{cone}}}\right) \]

\[ V_{\text{filled}} = \frac{\pi}{3} \cdot \text{H}_{\text{filled}} \cdot (br^2 + br \cdot R_{\text{cut}} + R_{\text{cut}}^2) \]

Case 2: If filled height > height of the conical section:

\[ V_{\text{filled}} = V_{\text{cone}} + \pi \cdot tr^2 \cdot (\text{H}_{\text{filled}} - H_{\text{cone}}) \]

Where:

H_filled = Height of the liquid level
H_cone = Height of the conical section
br = Bottom radius (diameter / 2)
tr = Top radius (diameter / 2)

Example Calculation

Suppose the tank has the following dimensions:

Bottom diameter = 10 m
Top diameter = 6 m
Cylindrical height = 5 m
Conical height = 4 m
Dome radius = 3 m

The total volume is calculated as:

1. \[ V_{\text{cylinder}} = \pi (5)^2 (5) = 125\pi \, \text{m}^3 \]

2. \[ V_{\text{cone}} = \frac{\pi}{3} (4) \left((5)^2 + 5 \cdot 3 + (3)^2\right) = \frac{\pi}{3} (4)(49) = \frac{196\pi}{3} \, \text{m}^3 \]

3. \[ V_{\text{dome}} = \frac{2}{3} \pi (3)^3 = 18\pi \, \text{m}^3 \]

Total Volume:

\[ V_{\text{tank}} = 125\pi + \frac{196\pi}{3} + 18\pi = \frac{659\pi}{3} \, \text{m}^3 \approx 690.8 \, \text{m}^3 \]

How can I convert the tank volume to liters?
1 m³ = 1,000 liters. Multiply the calculated volume by 1,000 to convert to liters.

What if the dome section is not a perfect hemisphere?
Adjust the dome volume formula based on the actual shape (e.g., spherical cap or custom geometry).

Can I use this formula for non-circular tanks?
No, this formula is specific to circular tanks. For non-circular tanks, use appropriate formulas for the geometry.