Cone Top Tank Volume Calculator - Calculate volume in litres, gallons, cubic feet, bbl, cubic meters

Tank Volume (m³):

Filled Volume (m³):

Tank Volume (U.S. Gallons):

Filled Volume (U.S. Gallons):

Tank Volume (Imp. Gallons):

Filled Volume (Imp. Gallons):

Tank Volume (Liters):

Filled Volume (Liters):

Tank Volume (Cubic Feet):

Filled Volume (Cubic Feet):

Tank Volume (bbl):

Filled Volume (bbl):

Cone Top Tank Volume Formula

Volume Calculation

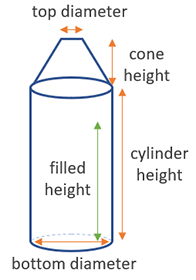
The volume of a cone top tank is calculated by determining the volume of the cylindrical section and the conical section. The total volume is given by:

\[ V_{\text{cylinder}} = \pi br^2 H_{\text{cyl}} \]

Where:

br = Bottom radius (bottom diameter / 2)
H_cyl = Height of the cylindrical section

\[ V_{\text{cone}} = \frac{\pi}{3} H_{\text{cone}} (br^2 + br \cdot tr + tr^2) \]

Where:

H_cone = Height of the conical section
br = Bottom radius (bottom diameter / 2)
tr = Top radius (top diameter / 2)

The total volume of the tank is the sum of the volumes of the cylindrical and conical sections:

\[ V_{\text{tank}} = V_{\text{cylinder}} + V_{\text{cone}} \]

Filled Volume Calculation

The filled volume of the tank is calculated using the formula:

If the filled height is less than or equal to the cylindrical height:

\[ V_{\text{filled}} = \pi br^2 H_{\text{filled}} \]

If the filled height is greater than the cylindrical height:

\[ R_{\text{cut}} = tr + \left(\frac{H_{\text{filled}} - H_{\text{cyl}}}{H_{\text{cone}}}\right) \cdot (br - tr) \]

\[ V_{\text{filled}} = \frac{\pi}{3} H_{\text{cone}} (br^2 + br \cdot R_{\text{cut}} + R_{\text{cut}}^2) + \pi br^2 H_{\text{cyl}} \]

Where:

H_filled = Filled height
H_cyl = Height of the cylindrical section
H_cone = Height of the conical section
br = Bottom radius (bottom diameter / 2)
tr = Top radius (top diameter / 2)

Why is the conical section's volume calculated separately?
The conical section has a different shape from the cylindrical section, requiring a separate formula that accounts for the tapering geometry.

How do you ensure accurate measurements of br and tr?
Measure the bottom and top diameters with a tape measure, and divide each by 2 to calculate the respective radii. Ensure measurements are taken at the widest points.

What if the tank is tilted?
For tilted tanks, adjustments must be made to the height dimensions (H_cyl and H_cone) using trigonometry to account for the change in effective height.

Can this formula be used for non-standard cone top tanks?
This formula assumes symmetrical cylindrical and conical sections. For non-standard shapes, approximate the sections as close as possible to these geometries or use numerical integration methods.

How does the formula handle partial fill volumes?
The formula adjusts based on the filled height. If the fill is within the cylindrical section, only that volume is calculated. If it extends into the cone, additional calculations for the conical section are included.